“常微分方程”的版本间的差异
| 第28行： | 第28行： | ||
齐次方程是可分离变量的：[[文件:常微分方程17.jpg]]，通解是y＝Ce<sup>-∫p(x)dx</sup>，令y＝c（x）e<sup>-∫p(x)dx</sup> 为（1）的解， | 齐次方程是可分离变量的：[[文件:常微分方程17.jpg]]，通解是y＝Ce<sup>-∫p(x)dx</sup>，令y＝c（x）e<sup>-∫p(x)dx</sup> 为（1）的解， | ||
| − | + | 即c（x）这时已不再是常数，y′＝c′（x）·e<sup>-∫p(x)dx</sup>－c(x)P（x）e<sup>-∫p(x)dx</sup>，代入（1）式消去两个相同的项得到c¢（x）＝Q（x）。e<sup>∫p(x)d</sup>。 | |
于是c（x）＝∫Q（x）e<sup>∫p(x)dx</sup>dx＋[[文件:常微分方程18.jpg]]。这时[[文件:常微分方程18.jpg]]是任意常数，最后得(2)的通解[[文件:常微分方程19.jpg]] | 于是c（x）＝∫Q（x）e<sup>∫p(x)dx</sup>dx＋[[文件:常微分方程18.jpg]]。这时[[文件:常微分方程18.jpg]]是任意常数，最后得(2)的通解[[文件:常微分方程19.jpg]] | ||
| 第42行： | 第42行： | ||
[[文件:常微分方程21.jpg]](a≠0，1)叫伯努利方程。令u＝y<sup>1-a</sup>，则可化为x和u的方程，且为线性方程，因而是可解的。 | [[文件:常微分方程21.jpg]](a≠0，1)叫伯努利方程。令u＝y<sup>1-a</sup>，则可化为x和u的方程，且为线性方程，因而是可解的。 | ||
| − | ⑥'''高阶常系数线性方程''' [[文件:常微分方程22.jpg]]（其中系数a1，a2，…，an是实常数）是可解的。以二阶方程为例来说明：[[文件:常微分方程23.jpg]]，（p，q为常数），它的求解归结为解代数方程：λ<sup>2</sup>＋pλ＋q＝0，设它的二根为（a）λ<sub>1</sub>≠λ<sub>2</sub>为实数，则通解为y＝c1[[文件:常微分方程24.jpg]]＋c2[[文件:常微分方程24.jpg]]；（b）λ<sub>1</sub>＝λ<sub>2</sub>为实数，则通解为y＝(c1x<sup>1</sup>＋c2)[[文件:常微分方程24.jpg]]，其中c<sub>1</sub>、c<sub>2</sub>为任意常数，（c）λ<sub>1,2</sub>＝α±βi为复数，则通解为y＝（c<sub>1</sub>cosβx＋c<sub>2</sub>sinβx）e<sup>ax</sup>。 | + | ⑥'''高阶常系数线性方程''' [[文件:常微分方程22.jpg]]（其中系数a1，a2，…，an是实常数）是可解的。以二阶方程为例来说明：[[文件:常微分方程23.jpg]]，（p，q为常数），它的求解归结为解代数方程：λ<sup>2</sup>＋pλ＋q＝0，设它的二根为（a）λ<sub>1</sub>≠λ<sub>2</sub>为实数，则通解为y＝c1[[文件:常微分方程24.jpg]]＋c2[[文件:常微分方程24.jpg]]；（b）λ<sub>1</sub>＝λ<sub>2</sub>为实数，则通解为y＝(c1x<sup>1</sup>＋c2)[[文件:常微分方程24.jpg]]，其中c<sub>1</sub>、c<sub>2</sub>为任意常数，（c）λ<sub>1,2</sub>＝α±βi为复数，则通解为y＝（c<sub>1</sub>cosβx＋c<sub>2</sub>sinβx）e<sup>ax</sup>。 |
| − | ⑦'''化为常系数方程法''' | + | ⑦'''化为常系数方程法'''——欧拉方程。 |
| − | + | ||
| + | [[文件:常微分方程26.jpg]] 令x＝e<sup>t</sup>，可化为 [[文件:常微分方程27.jpg]]，这已是常系数方程了（原式中a<sub>1</sub>与a<sub>2</sub>都是常数）。 | ||
| − | + | ⑧'''降阶法'''。有一些方程可通过某些变换化为较低阶方程，因而求解就方便了。例如，二阶变系数方程一般不可解：但若知方程y″＋P（x）y′＋q（x）y＝0的一个解y＝y<sub>1</sub>（x），令y＝y<sub>1</sub>（x）u（x），则可化为y<sub>1</sub>u″＋〔2y′<sub>1</sub>＋P（x）y<sub>1</sub>〕u′＝0。再令υ＝u?，则得到υ（x）的一阶方程，是可解的。 | |
| − | + | ⑨'''常系数线性非齐次方程'''：y″＋py′＋qy＝r（x）。此时可用常数变易法求解（因为齐次方程可解）还可用待定系数法!!!C0359_36当r（x）＝P（x）eax或〔P（x）cosβx＋Q（x）sinβx〕eax时，其中P（x）与Q（x）是多项式。 | |
| − | + | ||
| − | ⑨'''常系数线性非齐次方程''' | + | |
⑩'''常系数线性微分方程组''' | ⑩'''常系数线性微分方程组''' | ||
2017年3月2日 (四) 17:20的版本
常微分方程（ordinary equation），由一元函数得到的方程。即：称含有自变量，未知函数及其导数的关系式
为常微分方程。其中出现的最高阶导数的阶数，叫做常微分方程的阶。例如
，
，是一阶常微分方程，
是二阶常微分方程。
设y＝
（x）定义于区间J上，有直到n阶的导数，将它代入（1），使（1）变成关于x的恒等式，即
F（x，（x），
，…，
）≡0，x∈J
就称y＝（x）为（1）的一个定义于J上的解，并称J为该解的定义区间。
最简单的微分方程
，求解过程便是积分。
几种常见的初等解法（即把所给的微分方程化为积分形式）是：
①分离变量法。对微分方程
除以g(y），乘以dx化为dy／g(y）=f(x）dx此时，x和y各据一方，分离开来了，然后分别于两端对x和y积分得到“通积分”：
∫f（x）dx＋c，（解y＝（x）未写出，而是以隐式呈现的，就叫积分，一阶方程含有两个任意常数的解叫做通解）。
②变量替换法。例如，齐次方程为 
令y＝xu，则
，代入原式得，
＝f（u）－u。这时已经是分离变量型的方程了，变量替换可把“不会解”的方程变为已知求解法的方程。
③常数变易法。例如一阶线性方程
当
时，叫非齐次线性方程，
时叫齐次线性方程。
齐次方程是可分离变量的：
，通解是y＝Ce-∫p(x)dx，令y＝c（x）e-∫p(x)dx 为（1）的解，
即c（x）这时已不再是常数，y′＝c′（x）·e-∫p(x)dx－c(x)P（x）e-∫p(x)dx，代入（1）式消去两个相同的项得到c¢（x）＝Q（x）。e∫p(x)d。
于是c（x）＝∫Q（x）e∫p(x)dxdx＋
。这时是任意常数，最后得(2)的通解
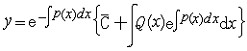
④全微分方程法。设给出微分方程为
P(x，y)dx＋Q(x，y)dy＝0 （3）
若存在一个二元函数u（x，y）＝c,使 
，则u（x，y）＝c便是（3）的通积分。
⑤积分因子法。当（3）不是全微分方程，但存在一个函数μ（x，y），使μ（x，y）P（x，y）dx＋μ（x，y）Q（x，y）dy＝0是全微分方程时，则称μ（x，y）为（3）的一个积分因子，找积分因子，从而得到的解（或积分）的方法叫积分因子法。
(a≠0，1)叫伯努利方程。令u＝y1-a，则可化为x和u的方程，且为线性方程，因而是可解的。
⑥高阶常系数线性方程 
（其中系数a1，a2，…，an是实常数）是可解的。以二阶方程为例来说明：
，（p，q为常数），它的求解归结为解代数方程：λ2＋pλ＋q＝0，设它的二根为（a）λ1≠λ2为实数，则通解为y＝c1
＋c2；（b）λ1＝λ2为实数，则通解为y＝(c1x1＋c2)，其中c1、c2为任意常数，（c）λ1,2＝α±βi为复数，则通解为y＝（c1cosβx＋c2sinβx）eax。
⑦化为常系数方程法——欧拉方程。
令x＝et，可化为 
，这已是常系数方程了（原式中a1与a2都是常数）。
⑧降阶法。有一些方程可通过某些变换化为较低阶方程，因而求解就方便了。例如，二阶变系数方程一般不可解：但若知方程y″＋P（x）y′＋q（x）y＝0的一个解y＝y1（x），令y＝y1（x）u（x），则可化为y1u″＋〔2y′1＋P（x）y1〕u′＝0。再令υ＝u?，则得到υ（x）的一阶方程，是可解的。
⑨常系数线性非齐次方程：y″＋py′＋qy＝r（x）。此时可用常数变易法求解（因为齐次方程可解）还可用待定系数法!!!C0359_36当r（x）＝P（x）eax或〔P（x）cosβx＋Q（x）sinβx〕eax时，其中P（x）与Q（x）是多项式。
⑩常系数线性微分方程组 !!!C0359_37 归结为求特征方程 !!!C0359_38 的根λ1，λ2，…，λn及与之相应的特征向量的问题，在四阶以下一般是可能计算的。当有重根时，利用矩阵的级当标准形，仍可求得通解。首次积分法：设给出方程组!!!C0359_39＝fi（x，y1，y2，…，yn）（i＝1，2，…，n）
（4） 其中右端函数f1，f2，…，f1在某区域D!!!C0359_40Rn+1内连续，关于y1，…，yn可微,设函数Φ（x，y1，…，yn）在G!!!C0359_41D内可微，不是常数，但沿着（4）的任一解C：y1＝y1（x），…，yn＝yn（x）（x∈J），Φ≡c，C为常数，则称Φ＜c为（4）的一个首次积分。首次积分在常微分方程中可算一个独立课题，也可通过它求解常微分方程组，例如前述的二体问题。 1841年J.刘维尔证明黎卡提方程!!!C0359_42除υ＝0，1，2，…时有初等解，其他情况一般没有初等解，从理论上结束了求通解的尝试。相继发明了数值计算法（发展为计算数学的一部分）、定性理论、稳定性理论，在近代发展成若干前沿分支：分支理论，动力系统等。这首先要解决存在性问题，有柯西定理、毕卡定理等。
