拓扑学
拓扑学(英语:Topology),数学中研究连续性现象的分支学科。拓扑学研究拓扑空间在同胚(拓扑)变换下不变的性质。同胚变换是指连续变换,且其逆映射也存在连续。从直观上看是研究图形在这样的形变下保持不变的性质:图形可作任意弯曲、拉大或缩小形变,只要形变过程中原来的点不粘为一点,也不产生新的点。拓扑学一词是由表示位置的拓扑斯(Topos)和表示理念意义的词逻格斯(Logos)这两个希腊语词汇合成的。最早(1847年)用于在J.B.里斯廷的《拓扑学初步》一文中。
概述
拓扑学起初是几何学的一支,研究几何图形在连续变形下保持不变的性质(所谓连续变形,形象地说就是允许伸缩和扭曲等变形,但不许割断和粘合);现在已发展成为研究连续性现象的数学分支。由于连续性在数学中的表现方式与研究方法的多样性,拓扑学又分成研究对象与方法各异的若干分支。在拓扑学的孕育阶段,19世纪末,就已出现点集拓扑学与组合拓扑学两个方向。现在前者已演化成一般拓扑学,后者则成为代数拓扑学。后来,又相继出现了微分拓扑学、几何拓扑学等分支。拓扑学主要是由于分析学和几何学的需要而发展起来的,它自20世纪30年代以来的大发展,尤其是它的成果与方法对于数学的各个领域的不断渗透,是20世纪理论数学发展中的一个明显特征。
最初的拓扑学定理是1736年L.欧拉发表的关于柯尼斯堡七桥问题的解答,且给出了连通网络一笔画的充要条件。1750年他又给出了多面体的欧拉定理断言与二维球面S2同胚(即能连续形变为S2)的多面体的顶点数a0、棱数a1、面数a2满足a0-a1+a2=2,此数称为S2的欧拉示性数。用它可以证明凸正多面体只有正四面体、正八面体、正十二面体、正六面体、正二十面体五种。它在闭曲面的分类问题,四色问题的证明中都起了很大的作用。继欧拉之后,1833年前后C.F.高斯研究空间各种纽结(即打结的非自交的闭曲线),研究结能否打开;两个结能否互相形变,即纽结的等价分类问题。高斯给出了闭曲线的环绕数,这是纽结理论研究的基本工具之一。均为拓扑学萌芽阶段的研究成果。
1895年B.黎曼提出了黎曼面的概念。他在研究复变函数时,开始对曲面拓扑性质进行系统研究。解决了定向闭曲面的分类问题,且给出了n维流形的确切定义。
J.-H.庞加莱是公认的组合拓扑的奠基人。1895年他以《关于位置几何学》为题发表的数篇论文,是对拓扑空间进行代数研究的开始。
拓扑学的另一分支点集拓扑学渊源于数学分析奠基工作及泛函分析的产生。19世纪末G.康托尔建立了集合论,且进一步定义了欧几里得空间的开集、闭集、导集等,获得了欧几里得空间拓扑结构的重要结果。以后泛函分析的兴起,更促进了把点集当作空间来研究。
微分拓扑起源于庞加莱猜想,1936年H.惠特尼关于嵌入定理发表以后开始形成一个独立的数学分支。
拓扑学渗透到数学各分支,如同调群、同伦群的研究促进了同调代数的发展;纤维丛、微分流形,微分拓扑的研究促进了微分几何的发展;微分动力体系是微分拓扑与微分方程交叉的学科。不仅如此,拓扑学已被广泛应用于物理、化学、生物、经济等学科。纽结应用于物理及遗传工程就是其中一例。
拓扑问题的一些初等例子
七桥问题(一笔画问题)
柯尼斯堡是东普鲁士首府,普莱格尔河横贯其中,上有七座桥。一个散步者怎样才能走遍七座桥而每座桥只经过一次?这个18世纪的智力游戏,被L.欧拉简化为用细线画出的网络能否一笔画出的问题,然后他证明这是根本办不到的。一个网络之能否一笔画出,与线条的长短曲直无关,只决定于其中的点与线的连接方式。设想一个网络是用柔软而有弹性的材料制作的,在它被弯曲、拉伸后,能否一笔画出的性质是不会改变的。
欧拉的多面体公式与曲面的分类
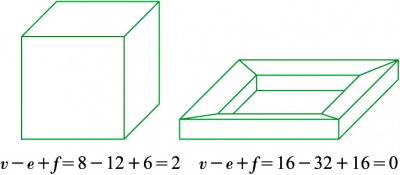
欧拉发现,不论什么形状的凸多面体,其顶点数v、棱数e、面数f之间总有v-e+f=2这个关系。从这个公式可以证明正多面体只有5种。值得注意的是,如果多面体不是凸的而呈框形(图1),也不管框的形状如何,总有v-e+f=0。这说明,凸形与框形之间有比长短曲直更本质的差别,通俗的说法是框形里有个洞。
在连续变形下,凸体的表面可以变为球面,框的表面可以变为环面(轮胎面)。这两者却不能通过连续变形互变。在连续变形下封闭曲面有多少种不同类型?怎样鉴别它们?这曾是19世纪后半叶拓扑学研究的主要问题。把曲面变形成多面体后的欧拉数v-e+f在其中起着关键的作用。见闭曲面的分类。
四色问题
在平面或球面上绘制地图,有公共边界线的区域用不同的颜色加以区别。19世纪中期,人们从经验猜想用4种颜色就足以给所有的地图上色。证明这个猜想的尝试,却延续了100多年,到1976年才出现了一个借助于计算机的证明。如果不是在平面上而是在轮胎面上画地图,四色就不够了,要七色才够。用橡皮做一个曲面模型,然后随意扭曲,弄得山峦起伏,这对其上的地图着色毫无影响,所以这颜色数也是曲面在连续变形下不变的性质。
纽结问题
空间中一条自身不相交的封闭曲线,会发生打结现象。要问一个结能否解开(即能否变形成平放的圆圈),或者问两个结能否互变(例如,图2中的两个三叶结能否互变),并且不只做个模型试试,还要给出证明,那就远不是件容易的事了。见纽结理论。
维数问题
什么是曲线?朴素的观念是点动成线,随一个参数(时间)连续变化的动点所描出的轨迹就是曲线。可是,G.皮亚诺在1890年竟造出一条这样的“曲线”,它填满整个正方形!这激发了关于维数概念的深入探讨,经过20~30年才取得关键性的突破。见维数。
布线问题(嵌入问题)
一个复杂的网络能否布在平面上而不自相交叉?做印刷电路时自然会碰到这个问题。图3中左面的图把一根对角线移到方形外面就可以布在平面上,但图4两个图却无论怎样挪动都不能布在平面上。1930年K.库拉托夫斯基证明,一个网络是否能嵌入平面,就看其中是否不含有这两个图之一。
向量场问题
考虑光滑曲面上的连续的切向量场,即在曲面的每一点放一个与曲面相切的向量,并且其分布是连续的。其中向量等于0的地方称为奇点。例如,地球表面上每点的风速向量就组成一个随时间变化的切向量场,而奇点就是当时没风的地方。从直观经验看出,球面上的连续切向量场一定有奇点,而环面上却可以造出没有奇点的向量场。
进一步分析,每个奇点有一个“指数”,即当动点绕它一周时,动点处的向量转的圈数;此指数有正负,视动点绕行方向与向量转动方向相同或相反而定(图5)。H.庞加莱发现,球面上切向量场,只要奇点个数是有限的,这些奇点的指数的代数和(正负要相消)恒等于2;而环面上的则恒等于0。这2与0恰是那两个曲面的欧拉数,这不是偶然的巧合。
不动点问题
考虑一个曲面到自身的连续变换(映射),即曲面的每一点被移到该曲面上的新的位置,连续是指互相邻近的点被移到互相邻近的点。新旧位置相同的点称为这变换的不动点。每个不动点也有个“指数”,即当动点绕它一周时,从动点指向其像点的向量转动的圈数。拓扑学家们发现,曲面到自身的映射的不动点个数如果是有限的,它们的指数的代数和不会因对这映射作细微的修改而改变,因而可从这映射的某些粗略的特征计算出来。特别是对于实心圆上的映射,指数和恒为1,所以实心圆到自身的映射总有不动点。这类定理对于证明数学中各种方程的解的存在性非常有用。
以上这些例子启示了:几何图形还有一些不能用传统的几何方法来研究的性质。这些性质与长度、角度无关,它们所表现的是图形整体结构方面的特征。这种性质也就是图形的所谓拓扑性质。
拓扑学所谈论的几何图形,不限于现实空间中的形体。如物理学中一个系统的所有可能的状态组成所谓状态空间,就是一个广义的几何图形。拓扑学是研究连续性的。变化的连续性,意思是它把邻近的点变成邻近的点。因此图形必须具有某种结构以表现点与点之间的邻近关系。规定了每两点间的距离并用距离大小来表示邻近关系的点集称为度量空间。最简单的例子是欧氏空间。然而在某些场合未必能规定出合用的距离,因而产生了拓扑空间与连续映射的概念。拓扑学中着重研究的是自然科学和数学中最常见的几类拓扑空间,如流形(光滑曲面的推广)、复形(多面体的推广)等。
前面所说的几何图形的连续变形,确切的含义是同胚。如果映射f: A→B是图形A的点与图形B的点之间的一对一的对应,而且f同它的逆映射f−1: B→A都是连续的,就说图形A与图形B同胚。这时从拓扑学的观点看A与B的结构相同,不必加以区别。例如,三角形与圆形同胚;而直线与圆周不同胚,因为直线挖去一点后不连通,而圆周挖去一点后仍连通。
拓扑学的一个典型问题,是问两个给定的几何图形是否同胚;引申一下,是要把图形按照同胚与否加以分类,并找出刻画每一个类的特征。一般的想法是,赋予每个图形以一些量(广义的量可以是数,如维数、欧拉数,可以是代数结构,如群、环,也可以是性质,如连通性、紧性),使得同胚的图形具有相同的量。这样的量称为拓扑不变量或同胚不变量(欧拉多面体公式中的数v、e、f都不是同胚不变量,而欧拉数v-e+f则是)。拓扑不变量帮助鉴别不同胚的图形,如球面与环面的欧拉数不同,它们就不同胚。
许多重要的几何现象,需要用连续映射来描述,因此连续映射也是拓扑学的主要研究对象。一个典型的问题,是问两个给定的映射是否同伦,即问两个映射h0,h1:A→B能否用连续地随时间t改变的一族映射{ht:A→B}0≤t≤1连接起来。与前相仿,从同伦问题产生了同伦不变量的概念。例如,从圆周到圆周的两个映射是否同伦,决定于它们的“度”(即当动点绕行一周时其像点绕行的圈数)是否相同,“度”就是一个同伦不变量。
发展简史
拓扑学起初叫形势分析学,这是G.W.莱布尼茨1679年提出的名词(中文译成形势,形指一个图形本身的性质,势指一个图形与其子图形相对的性质,纽结和嵌入问题就是势的问题)。L.欧拉1736年解决了七桥问题(见图论),1750年发表了多面体公式;C.F.高斯1833年在电动力学中用线积分定义了空间中两条封闭曲线的环绕数。拓扑学这个词(中文是音译)是J.B.利斯廷提出的(1847),源自希腊文τοπος(位置、形势)与λογος(学问)。这是萌芽阶段。
1851年起,B.黎曼在复函数的研究中提出了黎曼面的几何概念,并且强调,为了研究函数,研究积分,就必须研究形势分析学。从此开始了拓扑学的系统研究,黎曼本人解决了可定向闭曲面的同胚分类问题。在几何学的研究中黎曼明确提出n维流形的概念(1854)。
组合拓扑学的奠基人是H.庞加莱。他是在分析学和力学的工作中,特别是关于复函数的单值化和关于微分方程决定的曲线的研究中,引向拓扑学问题的,他的主要兴趣在n维流形。在1895~1904年间,他创立了用剖分研究流形的基本方法。他引进了许多不变量:基本群、同调、贝蒂数、挠系数,并提出了具体计算的方法。他探讨了三维流形的拓扑分类问题,提出了著名的庞加莱猜想。他留下的丰富思想影响深远,但他的方法有时不够严密,过多地依赖几何直观。
拓扑学的另一渊源是分析学的严密化。实数的严格定义推动G.康托尔从1873年起系统地展开了欧氏空间中的点集的研究,得出许多拓扑概念,如聚点(极限点)、开集、闭集、稠密性、连通性等。在点集论的思想影响下,分析学中出现了泛函数(即函数的函数)的观念,把函数集看成一种几何对象并讨论其中的极限。这终于导致抽象空间的观念。这样,到19、20世纪之交,已经形成了组合拓扑学与点集拓扑学这两个研究方向。
一般拓扑学
最早研究抽象空间的是M.-R.弗雷歇,在1906年引进了度量空间的概念。F.豪斯多夫在《集论大纲》(1914)中用开邻域定义了比较一般的拓扑空间,标志着用公理化方法研究连续性的一般拓扑学的产生。随后波兰学派和苏联学派对拓扑空间的基本性质(分离性、紧性、连通性等)做了系统的研究。经过20世纪30年代中期起布尔巴基学派的补充(一致性空间、仿紧性等)和整理,一般拓扑学趋于成熟,成为第二次世界大战后数学研究的共同基础。从其方法和结果对于数学的影响看,紧拓扑空间和完备度量空间的理论是最重要的。紧化问题和度量化问题也得到了深入的研究。
欧氏空间中的点集的研究,一直是拓扑学的重要部分,已发展成一般拓扑学与代数拓扑学交汇的领域,也可看作几何拓扑学的一部分。20世纪50年代以来,以R.H.宾为代表的美国学派的工作加深了对流形的认识,在四维庞加莱猜想的证明中发挥了作用。从皮亚诺曲线引起的维数及连续统的研究,习惯上也看成一般拓扑学的分支。
代数拓扑学
L.E.J.布劳威尔在1910~1912年间提出了用单纯映射逼近连续映射的方法,用以证明了不同维的欧氏空间不同胚,引进了同维流形之间的映射的度以研究同伦分类,并开创了不动点理论。他使组合拓扑学在概念精确、论证严密方面达到了应有的标准,成为引人瞩目的学科。紧接着,J.W.亚历山大1915年证明了贝蒂数与挠系数的拓扑不变性。
随着抽象代数学的兴起,1925年左右E.诺特提议把组合拓扑学建立在群论的基础上,在她的影响下H.霍普夫1928年定义了同调群。从此组合拓扑学逐步演变成利用抽象代数的方法研究拓扑问题的代数拓扑学。S.艾伦伯格与N.E.斯廷罗德1945年以公理化的方式总结了当时的同调论,后写成《代数拓扑学基础》(1952),对于代数拓扑学的传播、应用和进一步发展起了巨大的推动作用。他们把代数拓扑学的基本精神概括为:把拓扑问题转化为代数问题,通过计算来求解。同调群,以及在20世纪30年代引进的上同调环,都是从拓扑到代数的过渡(见同调论)。直到今天,同调论(包括上同调)所提供的不变量仍是拓扑学中最易于计算的,因而也最常用的。
同伦论研究空间的以及映射的同伦分类。W.赫维茨1935~1936年间引进了拓扑空间的n维同伦群,其元素是从n维球面到该空间的映射的同伦类,一维同伦群恰是基本群。同伦群提供了从拓扑到代数的另一种过渡,其几何意义比同调群更明显,但是极难计算。同伦群的计算,特别是球面的同伦群的计算问题刺激了拓扑学的发展,产生了丰富多彩的理论和方法。1950年J.-P.塞尔利用J.勒雷为研究纤维丛的同调论而发展起来的谱序列这个代数工具,在同伦群的计算上取得突破,为其后拓扑学的突飞猛进开辟了道路。
从20世纪50年代末在代数几何学和微分拓扑学的影响下产生了K理论,解决了关于流形的一系列拓扑问题的时候起,出现了好几种广义同调论。它们都是从拓扑到代数的过渡,尽管几何意义各不相同,代数性质却都与同调或上同调十分相像,是代数拓扑学的有力武器。从理论上也弄清了,同调论(普通的和广义的)本质上是同伦论的一部分。
从微分拓扑学到几何拓扑学
微分拓扑学是研究微分流形与微分映射的拓扑学。J.-L.拉格朗日、B.黎曼、H.庞加莱早就做过微分流形的研究;随着代数拓扑学和微分几何学的进步,在20世纪30年代重新兴起。H.惠特尼1935年给出了微分流形的一般定义,并证明它总能嵌入高维欧氏空间作为光滑的子流形。为了研究微分流形上的向量场,他还提出了纤维丛的概念,从而使许多几何问题都与上同调(示性类)和同伦问题联系起来了。
1953年R.托姆的协边理论开创了微分拓扑学与代数拓扑学并肩跃进的局面,许多困难的微分拓扑问题被化成代数拓扑问题而得到解决,同时也刺激了代数拓扑学的进一步发展。1956年J.W.米尔诺发现七维球面上除了通常的微分结构之外,还有不同寻常的微分结构。随后,不能赋以任何微分结构的流形又被人构作出来,这些都显示拓扑流形、微分流形以及介于其间的分段线性流形这三个范畴有巨大的差别,微分拓扑学也从此被公认为一个独立的拓扑学分支。1960年S.斯梅尔证明了五维以上微分流形的庞加莱猜想。J.W.米尔诺等人发展了处理微分流形的基本方法——剜补术,使五维以上流形的分类问题亦逐步趋向代数化。
近些年来,有关流形的研究中,几何的课题、几何的方法取得不少进展。突出的领域如流形的上述三大范畴之间的关系以及三维、四维流形的分类。20世纪80年代初的重大成果有:证明了四维庞加莱猜想,发现四维欧氏空间竟还有不同寻常的微分结构。这种种研究,通常泛称几何拓扑学,以强调其几何色彩,区别于代数味很重的同伦论。
拓扑学与其他学科的关系
连续性与离散性这对矛盾在自然现象与社会现象中普遍存在着,数学也可以粗略地分为连续性的与离散性的两大门类。拓扑学对于连续性数学自然是带有根本意义的,对于离散性数学也起着巨大的推进作用。拓扑学的基本内容已经成为现代数学工作者的常识。拓扑学的重要性,体现在它与其他数学分支、其他学科的相互作用。
拓扑学与微分几何学有着血缘关系,它们在不同的层次上研究流形的性质。为了研究黎曼流形上的测地线,H.M.莫尔斯在20世纪20年代建立了非退化临界点理论,把流形上光滑函数的临界点的指数与流形本身的贝蒂数联系起来,并发展成大范围变分法。莫尔斯理论后来又用于拓扑学中,证明了典型群的同伦群的博特周期性(这是K理论的基石),并启示了处理微分流形的剜补术。微分流形、纤维丛、示性类给É.嘉当的整体微分几何学提供了合适的理论框架,也从中获取了强大的动力和丰富的课题。陈省身在40年代引进了“陈氏示性类”,就不但对微分几何学影响深远,对拓扑学也十分重要。纤维丛理论和联络论一起为理论物理学中杨–米尔斯规范场论提供了现成的数学框架,犹如20世纪初黎曼几何学对于A.爱因斯坦广义相对论的作用。规范场的研究又促进了四维的微分拓扑学出人意料的进展。
拓扑学对于分析学的现代发展起了极大的推动作用。随着科学技术的发展,需要研究各式各样的非线性现象,分析学更多地求助于拓扑学。20世纪30年代J.勒雷和J.P.绍德尔把L.E.J.布劳威尔的不动点定理和映射度理论推广到巴拿赫空间形成了拓扑度理论。后者以及前述的临界点理论,都已成为研究非线性偏微分方程的标准的工具。微分拓扑学的进步,促进了分析学向流形上的分析学(又称大范围分析学)发展。在R.托姆的影响下,微分映射的结构稳定性理论和奇点理论已发展成为重要的分支学科。S.斯梅尔在60年代初开始的微分动力系统的理论,就是流形上的常微分方程论。M.F.阿蒂亚等人60年代初创立了微分流形上的椭圆型算子理论。著名的阿蒂亚–辛格指标定理把算子的解析指标与流形的示性类联系起来,是分析学与拓扑学结合的范例。现代泛函分析的算子代数已与K理论、指标理论、叶状结构密切相关。在多复变函数论方面,来自代数拓扑的层论已经成为基本工具。
拓扑学的需要大大刺激了抽象代数学的发展,并且形成了两个新的代数学分支:同调代数学与代数K理论。代数几何学从20世纪50年代以来已经完全改观。托姆的协边论直接促使代数簇的黎曼–罗赫定理的产生,后者又促使拓扑K理论的产生。现代代数几何学已完全使用上同调的语言,代数数论与代数群也在此基础上取得许多重大成果,例如有关不定方程整数解数目估计的韦伊猜想和莫德尔猜想的证明。
范畴与函子的观念,是在概括代数拓扑的方法论时形成的。范畴论已深入数学基础、代数几何学等分支;对拓扑学本身也有影响,如拓扑斯的观念大大拓广了经典的拓扑空间观念。
在经济学方面,J.冯·诺伊曼首先把不动点定理用来证明均衡的存在性。在现代数理经济学中,对于经济的数学模型,均衡的存在性、性质、计算等根本问题都离不开代数拓扑学、微分拓扑学、大范围分析的工具。在系统理论、对策论、规划论、网络论中拓扑学也都有重要应用。
托姆以微分拓扑学中微分映射的奇点理论为基础创立了突变理论,为从量变到质变的转化提供各种数学模式。在物理学、化学、生物学、语言学等方面已有不少应用。
除了通过各数学分支的间接的影响外,拓扑学的概念和方法对物理学(如液晶结构缺陷的分类)、化学(如分子的拓扑构形)、生物学(如DNA的环绕、拓扑异构酶)都有直接的应用。
拓扑学与各数学领域、各科学领域之间的边缘性研究方兴未艾。