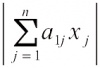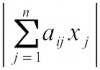几何数论
来自中文百科,文化平台
(重定向自数的几何)
几何数论(英语:geometric number theory),应用几何方法研究某些数论问题的数论分支。又称数的几何。它开始于17~18世纪间J.-L.拉格朗日和C.F.高斯等以几何观点研究二次型的算术性质的工作,最终于19世纪末叶由于H.闵可夫斯基的奠基性工作而创立,并且成为丢番图逼近,代数数论研究的重要工具。
用Rn表示n维实欧几里得空间,Rn中坐标(x1,x2,…,xn)为整数的点x称为(n维)整点(或格点)。对于Rn的子集K,若x∈K则必有−x∈K,那么,称K关于原点对称(简称对称)。如果连接K中任何两点的线段均含在K中,则称K为凸集。闵可夫斯基研究了对称凸集的基本性质,得到数的几何第一基本定理:如果Rn的子集K是体积为V(可能为无穷)的对称凸集,且V≥2n,那么,在K内或边界上必有一个非零整点。由此可得闵可夫斯基线性型定理:设c1,…,cn是正实数,aij(1≤i,j≤n)是实数,如果c1·…·cn≥
,那么,存在非零整点 x=( x1,…, xn)满足不等式组
≤ c 1, < c i,( i=2,…, n)
应用这个定理可以得到丢番图逼近的一系列结果。例如,对于 n个实数 a1,…, an,若其中至少有一个无理数,则有无穷多个有理数组( p1 / q,…, pn/ q),适合
< q -(1+1/n),(1≤ i≤ n)。此外,上述定理还可用来解决 代数数域 的基本单位问题。
闵可夫斯基还研究了K中所含线性无关的整点的分布,所得结果称为数的几何第二基本定理。20世纪70年代W.M.施密特以它为主要工具解决了实代数数联立有理逼近问题。
数的几何还研究用给定凸集覆盖或填装某个集合的问题,它们在编码理论和离散数学中有实际应用。