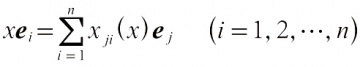李群
李群(英语:Lie group),由挪威数学家M.S.李创立的一类群。抽象群G若是一个实(复)解析流形,且对于任意x,y∈G,(x,y)→xy−1所定义的G×G到G的映射是一个解析映射,则称G是一个李群。
例如:
①一般线性群GL(n,R),或GL(n,C),是n维实(复)向量空间V上全体自同构(可逆线性变换)作成的群,它是一个李群。在向量空间V上取一组基e1,e2,…,en任一x∈GL(n,R)便有
:
矩阵(xij(x))n×n是非奇异的,x7(xij(x))n×n便使GL(n,R)成为解析流形。
②SL(n,R)(SL(n,C))称为幺模线性群,它是GL(n,R)(GL(n,C))中矩阵的行列式为1的集合构成的群。
③令(ξ,η)是向量空间V上的一个非奇异双线性型,于是在GL(n,R)(GL(n,C))中使(xξ,xη)=(ξ,η)的所有x的集合构成群。当(ξ,η)是正定对称时,称为正交群O(n,R)(O(n,C));当(ξ,η)是反对称时,称为辛群SP(n,R)(SP(n,C))。以上这些群都称为R(C)上典型群,它们都是李群。
李群的李代数
李的重要贡献是引进了李代数的概念。令G是一个李群,考虑流形G上的左(右)平移:设g∈G,它定义了G上的一个左乘变换x7gx,x∈G,称为由g定义的左平移τg。流形上的向量场是指流形上的微分算子X,于是流形上的左平移定义G的向量场间的“平移”。考虑G的左不变的向量场的集合g,在g内引进运算[X,Y]=XY-YX,X,Y∈g,这就赋予了g一个代数结构,称为对应于G的李代数。李代数的运算显然满足[X,Y]=−[Y,X]及雅可比恒等式[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0。任何非空集合若有一个运算,不妨也以记号[ ]来表达,且满足上面两个等式就称为李代数。
李得到下列基本定理:两个单连通李群同构的充分必要条件是它们有同构的李代数;任一抽象的李代数必为某单连通李群的李代数。由此看出李代数的讨论是李群理论的重要组成部分。李群理论的最基础的内容就是从李群的某些概念和性质找出对应李代数的性质。如李群间的同态对应于李代数的同态,李子群对应于子代数,正规子群对应于理想等。
分类问题
李群论中主要问题之一就是找出任意连通李群的所有的同构类。在具有同一李代数的所有局部同构的连通李群类中有唯一的单连通李群G0,而这一类的任意李群G都同构于G0/N,这里N是G0的中心的子群。这样李群的分类归结为有限维李代数的分类及单连通李群的中心的计算。李代数分为可解李代数和半单李代数。半单李代数的分类已完全解决,其中复的单李代数的分类由W.K.J.基灵和É.嘉当得到:有4个无限系列
An,n≥1;Bn,n≥2;Cn,n≥3;Dn,n≥4;
及5个例外李代数G2(14维),F4(52维),E6(78维),E7(133维),E8(248维)。
而复半单李代数是单李代数的直和。复单李代数的四个无限系列所对应的单连通李群有以下形式:
An型——SL(n+1,C);Bn型——Spin(f2n+1),是相应于一个2n+1维非奇异二次型f2n+1的旋量群;Cn型——2n次辛群;Dn型——Spin(f2n)。
不难计算出这些群的中心,实半单李群的分类可通过它们的实形式的分类来得到,可解李群的分类至今未有重要进展。
任意连通且单连通的李群G含有一个最大的正规连通可解闭子群称为它的根基,记为R,其商群G/R为半单李群。列维分解定理:G是R和与G/R同构的半单子群的半直积。
线性表示问题
李群G到GL(n,C)的一个同态连续对应称为G的一个线性表示。阿多定理:任一连通且单连通的李群必有一个忠实表示(与GL(n,C)的一个李子群同构)。
李群的线性表示归结为李代数的线性表示。É.嘉当和H.外尔已完全得到了紧半单李群的复线性表示的分类。
近代发展
李群与微分几何学、代数学、分析学是密切相关的。李群的近代理论有李群的无限维表示和调和分析、离散子群与自守函数论、齐性空间和其上的函数论、无限维李代数及一般域上李代数理论、李群理论推广到代数群等。
中国数学家严志达在李群的拓扑及实半单李代数分类的研究方面有突出贡献。