调和函数

　　调和函数（汉语拼音：Tiaohe Hanshu；英语：Harmonic Function），在平面区域D上定义的函数u＝u( x，y)，若有二阶连续偏导数，且满足二阶拉普拉斯方程则称u＝u（x，y）为D上的调和函数。调和函数与解析函数有密切关系，在平面区域D上的解析函数的实部与虚部都是调和函数，由于这一对调和函数还满足柯西黎曼条件，因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部，而且这样的解析函数不唯一，它们相互之间可以相差一个纯虚数，而在多连通区域上，一个调和函数一般是一个多值解析函数的实部。u（x，y）是区域D上调和函数的充要条件是u（x，y）在区域D连续且对D内任意一点P（x，y），存在正实数rp，对所有正数r<rp有其中cr是以P（x，y）为心，r为半径的圆，是u(x，y)沿cr法向的导数，当u（x，y）是一个圆盘△上的调和函数，且在上连续时，则u(x，y)在D内任一点的值可表为积分公式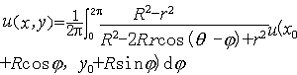：，R为D的半径，（x0，y0）为D的中心，（x，y）=（x0+rcosθ，y0+rsinθ），这一表达式称为波哇松积分公式。特别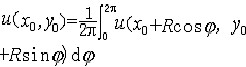，这一公式称为平均值公式，即u(x，y)在圆心的值是它在边界圆周上的值的算术平均值。由此公式可推知调和函数的极值原理：即区域D上非常数的调和函数在D内既不能达到局部极大值，也不能达到局部极小值。有许多实际问题可归结为求解调和函数的不同类型的边值问题，其中最基本的一类是狄里克莱边值问题，即求区域D内调和函数，使它连续到边，而在边界上取已给的边界值。二维区域上调和函数的定义与性质可以推广到n维区域的情形。