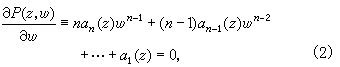代数函数
代数函数(英语:algebraic function),由不可约方程
确定的多值函数,式中 αj( z)( j=0,1,…, n)是 z的多项式。由(1)式和下列方程
消去 w得到的判别式 D( z)是 z的非恒为零的多项式。若 z0不是 D( z)的零点,则 p( z0, w)=0恰有 n个判别的根 wj( j=1,2,…, n)。
若再设 z0不是 αn( z)之零点,则由隐函数定理知,存在 n个判别的正则 函数元素( w j( z), B( z0))( j=1,2,…, n)属于方程(1),即在以 z0为心的某个圆 B( z0)内满足 P( z, wj( z))=0,且 wj( z0)= wj( j=1,2,…, n)。
若 z0是 D( z)之零点,则 P( z0, w)=0 有重根 wk,设其重级为 λk,且
此时在 z0点穿洞的小圆Ḃ( z0)上 n个 函数元素能分为 l个循环
(jk=1,2,…, λk, k=1,2,…, l)并且当沿着在Ḃ( z0)中的曲线围绕 z0开拓时,同一循环中的 函数元素互相置换。
设由 w1( z)在 Ḃ( z0)中开拓所得之多值 函数为 wλ( z),则它可表为某个圆 B( z0)内收敛的分数幂级数
此时( wλ( z), B( z0)),是属于方程(1) 的代数函数元素。当 z0= ∞ 时,以ζ=1/ z代之,若 w1= ∞,则以 u=1/ w代之。
再者由属于不可约方程(1)的任一函数元素(正则的或 代数的)出发可以用解析开拓方法来联接整个函数,即属于方程(1)的函数元素经解析开拓所得的函数元素仍属于方程(1),并且任两个属于方程(1)的函数元素能经解析开拓互相得到。因此代数函数是在扩充的复平面ĉ=C ∪{ ∞ }上仅具有有限多个代数分支点和极点的完全解析 函数。反之,具有上述特征的完全解析函数,且对于一固定点 z0,仅具有有限个以 z0为中心的函数元素者,满足一不可约代数方程,且除去一个非零的常数因子外,此方程是惟一的。
应用B.黎曼的方法可以构造一个新的曲面以代替z平面,使得在此曲面上代数函数为通常的单值函数,这个曲面即是黎曼曲面。相应于代数函数的黎曼曲面是紧的,曲面的亏格即定义为代数函数的亏格。
例如,超椭圆曲线w2=P(z)的亏格
其中 P(z)是 z的 m次多项式,[α]表示 α的整数部分。
由方程(1)联系着的z和w的有理函数R(z,w)之积分称为阿贝尔积分。
对于这个积分有一系列标准形式,使得任一这类型的积分能通过适当的变数变换变为其中一个标准形式。这个积分是一多值 函数,其多值性不仅产生于 R的留数和 w( z)的多值性,而且还依赖于相应的黎曼曲面的拓扑性质。
关于阿贝尔积分之研究还导致代数函数的单值化的可能性问题。代数函数单值化问题是对于方程(1)所确定的z和w的多值对应关系z↔w,去寻找一个参数表示(z(t),w(t)),其中z(t)和w(t)是定义于ĉ 的子域T上的t的单值函数。代数函数的单值化问题引起了一般单值化理论之发展。19世纪下半叶和20世纪的最初10年,世界上许多杰出的数学家,如黎曼、F.克莱因、H.庞加莱、H.A.施瓦兹、B.H.纽曼和P.克贝等人都作出了重要的贡献,最后于1908年由克贝和庞加莱同时解决。代数函数这个特殊情形的解决,曾引起拓扑学与共形映射理论之结合。对于代数函数单值化的基本结论是:亏格p=0的代数函数由有理函数单值化,即(z(t),w(t))是两个t的有理函数;亏格p=1时,由双周期椭圆函数单值化;亏格p≥2时,由单位圆内对某个富克斯群自守的亚纯函数单值化。
代数函数论还沿着算术的方向和几何的方向发展,后者是用几何方法研究代数曲线,并发展为代数几何。