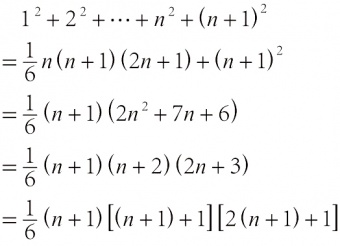数学归纳法
数学归纳法(mathematical induction),适用于论证与所有自然数有关的命题的归纳方法。与所有自然数有关的命题P(n)实际上是由无穷多个命题P(1),P(2),…,P(n),……所组成,采用逐个论证的方法是不可能完成的。数学归纳法依据的是自然数的“归纳公理”:假设M是自然数集N的子集,如果满足①1∈M。②当k∈M时能推出k+1∈M,那么M=N。由归纳公理可以导出数学归纳法原理:设P(n)是与所有自然数n有关的命题 ,如果①P(1)是真命题。②当P(k)是真命题时能推出P(k+1)也是真命题,那么对于任意自然数n,P(n)都是真命题。
数学归纳法的基本形式:对于与所有自然数有关的命题P(n),如果能:①证明命题P(1)成立。②假设对于任意自然数k,P(k)成立,证明P(k+1)也成立。则能断言命题P(n)对所有自然数n都成立。根据自然数集的“最小数原理”(即自然数集的每一个非空的子集必有最小数)可以推得数学归纳法的另一种形式(第二数学归纳法):对于与所有自然数有关的命题P(n),如果能:①证明命题P(1)成立。②假设对于任一自然数k,当1≤n≤k时 P(n)成立,证明P(k+1)也成立。则能断言对所有自然数n,命题P(n)都成立。
英文 mathematical induction 是英国数学家A.德·摩根于1838年提出的。对于依赖于自然数n=1,2,3,…的命题P(n),由于自然数有无穷多个,当然不能逐个验证。然而,如果当n=1时P(1)成立;又如果假定P(n)成立,可以推出P(n+1)成立,那么由P(1)成立可知P(1+1)即P(2)成立,由此可知P(2+1)即P(3)成立……如此递推,即可断定P(n)对一切n成立。以命题:
为例。当 n=1时,此式左端为 1 2=1,右端为:
故 P(1)成立。假定 P( n)成立,则对 n+1有:
即 P( n+1)成立。这就证明了所写命题对一切自然数 n成立。
上述论证方法的基础是能够被人们普遍接受的“公理”,即通称的数学归纳公理:设P(n)是依赖于自然数n的命题,如果①P(1)为真;②对任何自然数n, P(n)为真蕴涵P(n+1)为真,则P(n)对一切自然数n为真。(如果把0归入自然数,则①应改为P(0)为真)数学归纳公理等价于皮亚诺公理中的归纳公理。
基于数学归纳公理证明数学命题的方法,就是数学归纳法,又称完全归纳法。P(1)为真是归纳基础;假定P(n)为真,称为归纳假设;而由假设P(n)为真,证明P(n+1)为真,称为归纳步骤。
数学归纳公理有一个较弱的形式:设P(n)是依赖于自然数n的命题,如果①P(1)为真;②对任何自然数n,对一切小于n的自然数m为真蕴涵P(n)为真,则P(n)对一切自然数n为真。常称基于这种较弱形式的数学归纳公理证明数学命题的方法为第二数学归纳法;与之相对,前述方法称为第一数学归纳法。
数学归纳公理也是数学中归纳定义或归纳构造的基础。例如自然数加法的定义。以S(m)表示m的后继,对任何自然数m,定义m+1为S(m);如果m+n已有定义,则定义m+S(n)=S(m+n),也就是说m+n+1也有了定义。这样就对一切自然数n定义了。
数学归纳法的萌芽已出现在欧几里得《几何原本》(前300年前后)关于素数有无穷多个的证明中。1575年意大利数学家F.毛罗利库斯在所著《算术》中提出了这种方法并用来证明一些命题。法国数学家、物理学家、哲学家B.帕斯卡在所著《论算术三角形》(1654年印制,1655年发行)中相当清楚地阐述了这种方法。