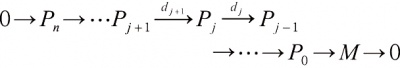同调代数学
来自中文百科,文化平台
(重定向自同调代数)
同调代数学(拼音:tóng diào dài shù xué;英语:homological algebra),20世纪40年代中期创立的代数学的重要分支,与代数拓扑学有紧密的关系。同调代数为环、群、李代数等代数结构的研究提供了有力的工具,在代数几何与代数拓扑等学科中也有重要应用。它研究的主要对象是模,但主要结果都可推广到更广的范畴。
任一环R上的左(右)R模M都有投射分解
式中一切 Pj 都是投射左 R模,即自由左 R模(有基模)的直和项,且左 R模同态 d j+1 的像与 dj 的核相等(即正合列,只要求 dj d j+1=0时称为 复形), j=0,1,…, n−1。上述 n<∞不存在时定义 M的左投射维数lpd( M)=∞, n<∞存在时上述分解与 n都不唯一,定义lpd( M)=inf{ n}。称lgD( R)=sup{ lpd M b M为左 R模}为 R的 左整体维数。类似地可定义 R的 右整体维数rgD( R)。lgD( R)=0等价于rgD( R)=0 即 R 为阿廷半单环;lgD( R)≤1(未必有rgD( R) ≤1)等价于 R为左遗传环(一切左理想都是投射模的环),从而给环性质一个有用的同调刻画。通过张量积可定义投射模的推广——平坦模并由此定义模的左(右)平坦维数及环 R的弱维数WD( R)。WD( R)=0等价于 R为正则环(即
,有 r′∈ R使 rr′ r= r)用张量积函子7与 同态函子Hom以及它们的导出函子Tor与Ext,可使这种理论更加完善,应用也更加方便。