坐标系
坐标系,数学、物理学、地理学、天文学等学科用语。定义如下: 对于一个n维系统,能够使每一个点和一组n个标量构成一一对应的系统。
坐标系可以用一个有序多元组表示一个点的位置。一般常用的坐标系,各维坐标的数字均为实数,但在高等数学中坐标的数字可能是复数,甚至是或是其他抽象代数中的元素(如交换环)。坐标系可以使几何学的问题转换为数字的问题,反之亦然,是解析几何学的基础。
在地理学中,描述地理位置时所用的经度及纬度构成一种地理坐标系。在天文学中,描绘天体在天球上位置的多种坐标系统是天球坐标系。在物理学中,描述一系统在空间中运动的参考坐标系统则称作参考系。
目录
常用的座标系
数线
数线是最简单的坐标系,用一个实数标示一个点在在线的位置。数线中会有一个原点O,以及单位长度及其方向。点P的坐标为从O到P的有号距离,坐标是正值或负值则依P点在原点的哪一侧来决定。数在线每一个点都有唯一的坐标,每一个实数也都可以在数在线找到唯一的对应点。
笛卡儿座标系
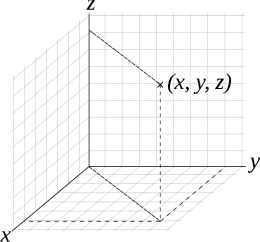
笛卡儿座标系也称为直角座标系,是最常用到的一种座标系。是法国数学家勒内·笛卡尔在1637年发表的《方法论》附录中提到的。
在平面上,选定二条互相垂直的线为座标轴,任一点距座标轴的有号距离为另一轴的座标,这就是二维的笛卡儿座标系,一般会选一条指向右方水平线称为x轴,再选一条指向上方的垂直线称为y轴,此两座标轴设定方式称为“右手座标系”。
若在三维系统中,选定三条互相垂直的平面,任一点距平面的有号距离为座标,二平面的交线为座标轴,即可产生三维的笛卡儿座标系。一般会选择x轴及y轴是水平的,z轴垂直往上,且三轴维持右手定则,若先将右手的手掌与手指伸直。然后,将中指指向往手掌的掌面 半空间,与食指呈直角关系。再将大拇指往上指去,与中指,食指都呈直角关系。则大拇指,食指,与中指分别表示了右手座标系的 x-轴,y-轴,与 z-轴。此概念可以延伸,在n维的欧几里得空间中建立n维的笛卡儿座标系。
以笛卡儿平面坐标系为基准,右上为第一象限,左上为第二,左下为第三,右下就是第四象限,第一象限的x坐标和y坐标均为正值,第二象限的x坐标为负值,y坐标为正值,第三象限的x坐标和y坐标均为负值,第四象限的x坐标为正值,y坐标为负值,而平面坐标分六大部分,除了四个象限,还有x轴与y轴。在笛卡儿空间坐标系中也可以依xy平面,xz平面及yz平面将不含上述平面空间分为八份,称为卦限,但一般只定义坐标均大于零的为第一卦限。坐标中的各轴线不属于象限或卦限。
极座标系

极座标系也是一种常用的平面座标系统。格雷瓜·德·圣-万桑特(Grégoire de Saint-Vincent)在1625年和博纳文图拉·卡瓦列里在1635年,独立地各自引入了极坐标系这一概念。极座标中会定一点为极点,再将一条通过极点的射线定为极轴。若给定一角度θ,则可绘出通过极点,和极轴夹角为θ的唯一射线(角度是以从极轴,依逆时针方向旋转到射线),若再给定一实数r,可找出上述射在线,距极点距离为有号整数r的一点。
在极座标系中,一座标(r, θ)只会其对应唯一的一点,但每一点均可对应许多个座标。例如座标(r, θ)、(r, θ+2π)及(−r, θ+π)都是对应同一点的不同座标。而极点的座标为(0, θ),θ可为任意值。
极坐标r 和 θ 可以用下式变换为直角坐标:
从直角坐标x和y也可以变换为极坐标:
若将平面上的极坐标系扩展到立体的空间,可扩展为圆柱座标系及球座标系。
圆柱座标系
圆柱座标系是将极坐标系的(r,θ)座标变成(ρ,ϕ),再增加一个笛卡尔座标系的z座标。如点P的圆柱座标是(ρ , ϕ , z)。
直角座标系和圆柱座标系的转换关系如下:
- x = ρ cos ϕ
- y =ρ sin ϕ
- z = z
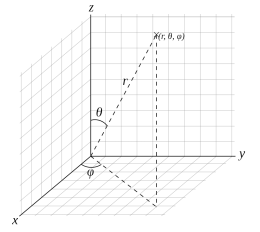
球座标系
球座标系是用一个角度 ϕ 表示原点到坐标点的连线与正z-轴之间的相对关系。如点P的球座标为(r, θ, ϕ)。
直角座标和球座标系的转换关系如下<ref name=nwpu/>:
- x = r sin θ cos ϕ
- y = r sin θ sin ϕ
- z = r cos θ
齐次坐标
在齐次座标表示时,会增加一个额外的座标,例如平面上的一点可以表示为(x, y, z),其中x/z及y/z为其原来在平面上的笛卡尔座标。其优点是可以在不使用无限大的情形下表示射影平面上的任意点。一般齐次座标会用在座标之间的比例比实际的数值来的重要的情形下。
其他常用坐标系
以下是其他一些常用的座标系:
- 曲线座标系(Curvilinear_coordinates)是一种广义的座标系,此座标系是以相交的曲线为基础。
- 广义座标是在处理拉格朗日力学时使用。
- 正则座标是在处理哈密顿力学时使用。
- 普吕克坐标可以将三维空间中的直线描述为6个齐次座标。
- 重心坐标一般用在三角图(Ternary plot)中。
- 平面上的对数-极座标系(Log-polar coordinates)是以用一点相对原点的角度及其距离的对数来表示。
- 平行座标将n-维空间中的一点表示为和n条垂直线有交点的折线。
可有一些描述曲线的方式和座标系无关,这类的方式会使用本征方程(intrinsic equation),其中有用到像是曲率及弧长等不随座标系而改变的不变量。这类的本征方程包括:
- 惠威尔方程(Whewell equation)和弧长和有关。
- 切萨罗方程(Cesàro equation)和弧长及曲率有关。
坐标转换
坐标转换是指在描述同一个空间时,由原来的座标系转换为另一个座标系。
对于每一个由空间到空间本身的对射,可定义二种坐标转换:
- 一种是每一个点在新座标系座标的对射,恰为旧座标系的座标。
- 一种是每一个点在旧座标系座标的对射,恰为新座标系的座标。
例如一维的系统中,若一映射为是往右移三个单位,则第一个座标转换会将原点从0移到3,因此每个点的座标都少了3,第二个座标转换会将原点从0移到-3,因此每个点的座标都多了3。
座标之间的转换有一定的公式。例如若平面上的笛卡尔座标(x, y)及极座标(r, θ)原点相同,则可以用以下的公式从极座标转换为笛卡尔座标:x = r cosθ及y = r sinθ。
其他几何形状的座标表示
座标系常用来描述一个点的位置,不过也可以用座标系描述其他复杂形状的位置,例如直线、平面、圆或是球等。例如普吕克座标就是用来描述空间中直线的位置。当有需要时,可以在座标系的前面加上需描述的形状做为识别,例如直线座标(line coordinates)就是指描述直线位置的座标。曲线为平行座标轴的直线。其他座标系的座标曲线就是一般的曲线。例如在极座标系中,若固定r为定值所形成的座标曲线是圆心在原点的圆。
坐标曲线及坐标曲面
若在二维座标系中一个座标维持定值,只允许一个座标变动,所形成的曲线称为座标曲线(或座标线)。不过不是所有的座标系都有座标曲线,例如齐次座标系中就没有座标曲线。
在欧几里得空间中笛卡尔座标系以外的座标系即称为曲线座标系(Curvilinear coordinates)。若在三维座标系中一个座标维持定值,允许其他座标变动,所形成的曲面称为座标曲面。例如在球座标系,若固定径向距离r为定值所形成的座标曲面是球心在原点的球。三维空间中二座标曲面的交线即为坐标曲线。在更高维度的空间也可依此定义座标超曲面。
参考系
在几何学及运动学中,座标系不但会用来描述点的直线位置,也会用来描述轴、正切角(tangential angle)平面或刚体的角度取向。一般会设定一固定于刚体的参考系,称为附体参考系。在笛卡尔座标系中,座标附体参考系,另一个不随刚体变动的参考则为空间参考系。一般刚体的运动可以在附体参考系下的座标来表示,再根据附体参考系相对空间参考系的位置及取向来取得刚体相对空间的运动。例如刚体的角度取向可以用一个方向矩阵来描述,矩阵的三个栏是三个点的笛卡尔座标,这些可用来标示局部座标系统的座标轴方向,也可用来计算座标轴的单位向量。
座标图
座标图(coordinate map)的概念是流形理论的核心。本质上座标图是一个针对给定空间子集的座标系,其中每一个点都恰有一个对应的座标。若要精准的定义,座标图可定义为从空间X的开子集到Rn的开子集的同胚。一般的座标系不太可能针对所有空间中的点都有明确唯一的座标。此时可以用一组座标图形成一个适合此空间的图册。有此性质的空间称为流形,若座标图重叠的部份符合某些特定的结构,也可以定义有特殊结构的流形。例如微分流形就是座标图之间的转换恒为微分函数的流形。