同伦论
同伦论(英语:homotopy theory),代数拓扑学的一个主要组成部分。它研究与连续映射的连续形变有关的各种内容。由于许多几何问题可以归结为同伦问题,然后谋求代数拓扑的解决办法,所以同伦论广泛地受到关注。
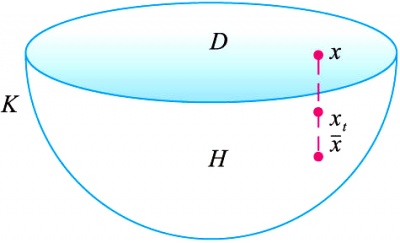
同伦的概念,直观上不难理解,同伦就是连续形变。以“形变收缩”为例,图中的半球体K的边界包括半球面H与圆盘D。设想K是由可以伸缩的质料构成,很显然,保持H上每个点不动,沿垂直于D的方向挤压K,最后可以将半球体K压成半球面H。也就是说,H是K的“形变收缩核”。这个形变收缩的过程可以描写得更确切一些。过K的任意点x垂直于圆盘D的直线与半球面H交于点x。对于0≤t≤1,令xt表示分线段xx为t:1-t之点。不妨认为挤压是从时刻t=0开始,到时刻t=1时完成,而时刻t时点x沿着线段xx到达xt的位置。使x对应于xt,定义了半球体K自身的一个连续映射ft:K→K,ft(x)=xt。于是,f0(x)=x0=x,f0为K自身的恒等映射,f1(x)1H,并且ft(y)=y,当y∈H,ft就是一个“伦移”,使得K自身的恒等映射同伦于一个将K映入子集H的映射。
设f,g:X→Y为拓扑空间X到Y的两个连续映射。如果有连续映射H:X×I→X,I=[0,1],使得h(x,0)=f(x),h(x,1)=g(x),则称f同伦于g,记作
在同伦论里,空间按同伦型而分类。如果存在连续映射f:X→Y,g:Y→X使得
,则称 X与 Y具有相同的同伦型,则称 f(或 g)为 同伦等价,这里, 1W: W→ W表示空间 W的恒等自映射。
同伦论的典型问题大体上有下列几个,以下映射均指连续映射。
同伦问题
对于给定映射f,g:X→Y,如何判断f与g是否同伦,如果f与常值映射同伦,则称f为零伦的,记作f-0。如何判断给定映射f是否零伦是这个典型问题的特例。
同调群提供了处理这个问题的工具。对任意整数n≥0,如果
,则 f *= g *∶ H n( X)→ H n( Y)。因此,如果对某一 n, f*≠ g *,则 f与 g一定不同 伦。但应注意,即使对所有 n, f *= g *, f与 g也未必同 伦。
扩张问题
设A1X,给定映射f:A→Y能否扩张为X到Y的映射,即是否存在映射g:X→Y,使得g(a)=f(a)(对一切a∈A)。如果存在这样的映射g,则称g为f在X上的扩张,而f为g在A上的限制,记作g;A=f。恒同映射1X在A上的限制
称为 A到 X的 内射。
提升问题
在研究流形上有没有非零向量场时,需要考虑映射的提升问题,它与扩张问题相对偶。提法如下:设p:X→B与f:Y→B是映射,是否存在映射g:Y→X,使得pg=f:Y→B。如果存在这样的映射g,则称g为f关于p的提升。是否存在g的问题就是提升问题。
同伦分类问题
对于给定空间X与Y,如何由X与Y的已知的可计算的不变量去计算从X到Y的映射同伦类集合[X,Y],这是代数拓扑学中经常碰到的问题,特别是同伦群的计算等。
如果X与Y满足一定的条件,则[X,Y]形成一个群。对n≥1及任意道路连通空间Y,W.赫维茨定义了πn(Y)=[Sn,Y]。可以证明πn(Y)是一个群,而且π1(X)就是H.庞加莱所定义的基本群。当n≥2,πn(Y)是交换群。从而把πn(Y)称为空间Y的n维同伦群,它也是同伦不变量。