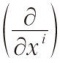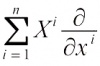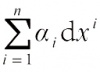微分流形
微分流形(英语:differentiable manifold),一类拓扑空间。除具有通常的拓扑结构外,还添上了微分结构。微分几何学的研究是建立在微分流形上的。三维欧氏空间 R3 中的曲面是二维的微分流形,但微分流形的概念远比这广泛得多,非但维数不限于二维,而且流形也不必作为n维欧氏空间 Rn 中的曲面来定义。此外,一般微分流形也不一定有距离的概念。
微分流形的主要特征是在每一点的邻域内有坐标系,并且在邻域重叠部分的坐标变换是可微的。具体地说,设M是豪斯多夫拓扑空间。如果对每一点p∈M,都有一个开邻域U以及从U到 Rn 的一个开子集的同胚 h:U→h(U)1Rn,则称M是一个n维拓扑流形。
这里的(U,h)称为点p的一个坐标卡,并且对于任意的q∈U,把h(q)在Rn中的分量称为点q的坐标,xi(q)=(h(q))i,同时把(U;xi)称为拓扑流形M的一个局部坐标系。
如果M是一个n维拓扑流形,并且有M的坐标卡的一个集合A={(Uα,hα):α∈Ⅰ},使得{Uα}构成M的开覆盖,
而且在 U α∩ U β≠ø时坐标变换函数
- x βi=( h β˚ h α −1) i( x 1 α,…, x n α)( i=1,2,…, n)
都是 hα (U α∩ U β)上的,有直到 k次的各阶连续偏导数的函数,则称( M,A)为 Ck微分流形,且称A为 M上的一个 Ck微分结构。 C ∞微分流形又称光滑流形。
如果M是一个光滑流形,并且能够取出M的容许的坐标卡集A1={(Vα,hα):α∈Ⅰ},使得{Vα}构成M的开覆盖,并且对于Vα∩Vβ≠ø,坐标变换hβ˚hα−1的雅可比矩阵在Vα∩Vβ上处处是正的,则称M是可定向的。
同一个拓扑流形可能具有本质上不同的光滑结构,1957年J.W.米尔诺在七维球面S7上首先发现这个事实。在20世纪80年代,M.H.弗里德曼等证明4维欧氏空间有多种光滑结构,而在其他维数的欧氏空间中只有唯一的微分结构。
光滑结构的主要功能是在光滑流形上可以定义光滑函数、切向量、切向量场和各阶张量场等数学对象。设 f:M → R 是M上的函数,若在点p∈M有容许的坐标卡(U,h),使仅f˚h−1是Rn的开子集h(U)上的光滑函数,则称f在点p是光滑的。在点p的光滑函数的全体构成的集合记为Cp∞。若f在M上每一点处都是光滑的,则称f是M上的光滑函数。M上的光滑函数的全体构成的集合记为C∞(M),设p∈M,M在点p的一个切向量v是指映射 v:Cp∞ →R,它满足条件①v(f+λg)=v(f)+λv(g);②v(f·g)=f(p)·v(g)+g(p)·v(f),式中f,g∈Cp∞,λ∈R。M在点p的切向量全体构成的集合记为TpM,它是一个向量空间,若(xi)是p点附近的局部坐标系,则
构成 T p M的基底。切空间 T p M的对偶空间记为 Tp * M,它的元素是 T p M上的线性函数,称为在点 p的 余切向量。 T p* M的基底由d x i( i=1,2,…, n)组成。
M上的光滑切向量场X在局部坐标系(xi)下可以表示为
,式中 X i是坐标域上的光滑函数。同样, M上的光滑余切向量场是
,式中 α i是坐标域上的光滑函数,它也称为 M 上的 一次微分式。更一般地, M上的 k次外微分式 ω的局部坐标表达式是
- ω= ω i1…ikd x i1/…/d x ik
式中 ωi1…ik是坐标域上的光滑函数。
光滑流形是许多数学分支的基础。例如在有第二可数公理的光滑流形上存在黎曼度量,而指定了黎曼度量的流形称为黎曼流形,该流形上展开的几何就是黎曼几何。在光滑流形上可以展开大范围分析的研究,其中特别著名的是德拉姆定理:光滑流形上由闭微分式给出的德拉姆上同调群与流形本身的(拓扑)上同调群是同构的。数学物理和力学的大范围研究也都是建立在微分流形理论的基础上的。