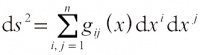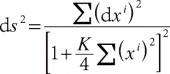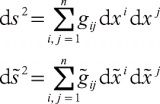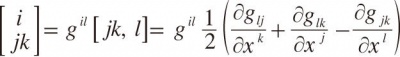微分几何学
微分几何学(英语:differential geometry),以微积分为主要研究工具的几何学,应用微分学来研究三维欧几里得空间中的曲线、曲面等图形性质的数学分支。差不多与微积分学同时起源于17世纪。单变量函数的几何形象是一条曲线,函数的导数就是曲线切线的斜率。函数的积分在几何上则可理解为一曲线下的面积等等。这种把微积分应用于曲线、曲面的研究,实质上就是微分几何学的开端。L.欧拉、G.蒙日、J.L.拉格朗日以及A.-L.柯西等数学家都曾为微分几何学的发展作出过重要贡献。与此同时,曲面内蕴几何等崭新的思想也在不断地产生并积累着。在此基础上,C.F.高斯奠定了曲面论基础,并使微分几何学成为一门新的数学分支。按F.克莱因变换群几何的分类方法来看,微分几何学应属于运动群,所以也称为运动几何学或初等微分几何学。
微分几何学的研究对数学其他分支以及力学、物理学、工程学等的影响是不可估量的。如:伪球面上的几何与非欧几何有密切关系;测地线和力学、变分学、拓扑学等有着深刻的联系,是内容丰富的研究课题。这方面有以J.阿达马、H.庞加莱等人为首的优异研究。极小曲面是和复变函数论、变分学、拓扑学关系极为深刻的研究领域,K.魏尔斯特拉斯、J.道格拉斯等人作出过卓越贡献。
微分几何学的研究工具大部分是微积分学。力学、物理学、天文学以及技术和工业的日益增长的要求则是微分几何学发展的重要因素。尽管微分几何学主要研究三维欧几里得空间中的曲线、曲面的局部性质,但它形成了现代微分几何学的基础则是毋庸置疑的。因为依赖于图形的直观性及由它进行类推的方法,即使在今天也未失其重要性。
微分几何起源于17世纪发明微积分的时候。函数和函数的导数在直观上就是曲线和曲线切线的斜率,函数的积分可解释为曲线下方图形的面积。经典的微分几何是研究三维欧氏空间中曲线和曲面的弯曲性质,以及确定它们的形状的(微分)不变量系统。首先作出贡献的是瑞士数学家L.欧拉。1736年,欧拉引进弧长参数作为曲线上的点的内在坐标,将曲线的切方向与一个固定方向夹角相对于弧长的变化率定义为曲线的曲率。在曲面论方面,他引进法曲率、主曲率、总曲率(高斯曲率),给出了法曲率的欧拉公式,和约翰第一·伯努利及丹尼尔第一·伯努利一起把测地线描述为某微分方程的解。法国数学家G.蒙日及其学派对曲面论也有很多贡献,在1807年出版了关于曲线、曲面论的第一部独立著作《分析学在几何中的应用》。在1847年弗雷内给出了曲线论基本公式——弗雷内公式。现在的曲面论第一基本形式和第二基本形式的记号是C.F.高斯在1827年的论文《关于曲面的一般研究》中提出的。高斯的这篇论文是划时代的作品,在其中他建立了曲面的两个基本形式必须满足的一个关系式,即现在所称的高斯方程。根据这个方程得知,曲面的两个主曲率的乘积(现称高斯曲率)只依赖曲面的第一基本形式,从而建立了曲面的内蕴微分几何,即在已知第一基本形式的情况下去研究曲面本身的弯曲性质,以及曲面内曲线的长度、夹角、所围面积和测地线等。
最重要的发展是B.黎曼在1854年的就职演说《关于几何学的基本假设》。在这篇演说中,他首先提出了n维流形(n重广延量)的概念,把n个实数(x1,x2,…,xn)看作空间中的点;在这种空间中没有直线的概念,但是在无限邻近的两点(xi)与(xi+dxi)(i=1,2,…,n)之间定义了距离的平方是
以此作为几何学的出发点。后来称(*)为黎曼度量,这里( gij)是正定对称阵。黎曼认识到,这种度量是加到流形上的一种结构,不是流形本身所固有的,而造成欧氏几何和非欧几何的差别的根源也就是这种度量的不同。黎曼给出的度量的公式是
这里 K是常数,当 K=0时对应的几何是欧氏几何, K<0时是双曲几何, K>0时是椭圆几何。黎曼几何的一个基本问题是等价问题,即两个二次微分形式
在什么条件下存在坐标变换: x˜ i= x˜ i( x1,…, xn)( i=1,2,…, n)将一个微分形式变到另一个微分形式。此问题在1869年由E.B.克里斯托费尔和R.李普希茨解决。在解决此问题时,克里斯托费尔引进了以他的名字命名的记号,即第一类克里斯托费尔记号[ jk,l]和第二类克里斯托费尔记号
- 以及协变微分的概念。在此基础上,G.里奇在1887~1896年发展了张量分析方法;他的学生T.列维–齐维塔发现了曲面上向量场沿曲线的平行移动。1901年里奇和列维–齐维塔的研究报告《绝对微分法》问世,这套理论在广义相对论中起到基本的作用。
1872年F.克莱因的就职演说提出后人所称的埃朗根纲领,把几何学定义为研究空间在某变换群作用下的不变量和不变性质的理论。这个指导原则推动了微分几何的发展,导致了射影微分几何学、仿射微分几何学和共形微分几何学的建立。但是,在一般的黎曼空间中,等距变换群是平凡的,因此难以纳入埃朗根纲领。后来,经过W.K.J.基灵和É.嘉当的努力,使得李群成为微分几何的有力工具,并且李群本身也成为微分几何的研究对象。由此发展出来的齐性黎曼流形和黎曼对称空间成为黎曼流形的重要例子和特别的课题。1916年,A.爱因斯坦提出广义相对论,黎曼几何及有关的算法(里奇的绝对微分法)成为广义相对论的有效的数学工具;此外,爱因斯坦还提出和式约定,简化了黎曼几何的符号系统。这样,黎曼几何很快成为数学研究的中心课题,黎曼流形成为弯曲空间的最主要模型。到现在为止,黎曼几何学仍然是现代微分几何学的主要组成部分。
H.外尔在1918年的名著《时间,空间,物质》中引进了仿射联络的概念,这是列维–齐维塔平行移动的推广,是在流形上比黎曼度量更基本的结构。经过嘉当、C.埃雷斯曼、J.-L.柯歇尔等人的努力,现在已经形成关于联络的完整理论,成为现代微分几何的重要组成部分。
从20世纪20年代以后,大范围微分几何,特别是大范围黎曼几何及大范围分析逐渐成为研究的重点,其中陈省身的“高斯–博内定理的内在证明“(1942)是大范围黎曼几何发展史上的里程碑,从此之后纤维丛、主纤维丛等概念占有显著的地位。黎曼流形的曲率和流形本身的拓扑结构的联系和互相制约成为十分重要的课题。
微分几何的研究和发展离不开微分方程,G.达布的《曲面论》一书就有丰富的古典微分方程的内容;嘉当和凯勒所发展的外微分方程理论为解析范围内的局部微分几何问题提供了一般的有效的方法。大范围微分几何更离不开现代分析工具。在线性理论中,一个突出的成果是阿蒂亚–辛格的指标定理。黎曼流形上的拉普拉斯算子的特征值研究也是一个重要方面。微分几何所遇到的偏微分方程大多是非线性的,在这方面,以丘成桐为代表,20世纪70年代的数学家开始系统地发展了偏微分方程理论在解决几何问题中的应用,已形成解决调和映射、极小子流形、共形度量、凯勒度量等存在性问题的几何分析的研究方向。微分几何学已经发展成为门类众多,与数学、物理的许多分支相互渗透的学科,并且成为研究拓扑学、复流形、非线性分析、函数论、数学物理的重要工具。