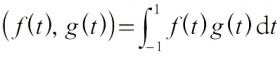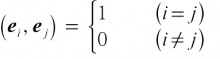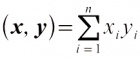欧几里得空间
欧几里得空间（英语：Euclidean space），带有“内积”的实数域上的一类向量空间。简称欧氏空间。“内积”是一个度量概念，有明显的代数性质，向量的长度和夹角都可以通过向量的内积来表示。所谓内积，是指与实数域R上向量空间E中任意一对向量u、v唯一对应的实数，这个实数记作(u,v),并满足以下条件：
①(u,v)=(v,u)；
②(u1+u2,v)=(u1,v)+(u2,v)；
③(au,v)= a(u,v)；
④(u,u)≥0,当且仅当u=0时(u,u)=0。式中u,u1,u2,v是E的任意向量，a是任意实数。
一个定义了内积的实数域上的向量空间，称为欧几里得空间。例如，设V是解析几何里的三维空间,u、v是V的任意向量，在V中定义(u,v)=|u|·|v|cosθ，式中|u|、|v|分别表示u、v的长度，θ表示u和v的夹角。(u,v)满足内积的全部条件, 所以V是一个欧氏空间。
设R是实数域，R上的n维向量空间Rn={(x1,x2,…,xn),|xi∈R,1≤i≤n},定义(x,y)=x1y1+x2y2+…+xnyn,式中x=(x1,x2,…,xn),y=(y1,y2,…,yn),则Rn成为一个欧氏空间。设E是定义在闭区间 [−1,1]上一切连续实函数所构成的向量空间，定义：
式中 f( t)、 g( t)是 E中的函数。则 E作成一个欧氏空间。
向量的长和夹角
欧氏空间E的一个向量x的长,定义为非负实数
，并记作| x|，即| x|=
。欧氏空间E的任意两个非零向量 x和 y的夹角 θ由公式cos θ=( x, y)/(| x|| y|)来确定。这是解析几何里关于两个向量夹角的自然推广。著名的柯西–施瓦兹不等式或布雅科夫斯基不等式( x, y)≤( x, x)( y, y),当且仅当 x与 y成比例时等号才成立,保证了上述的夹角定义的合理性。欧氏空间 E的两个向量 x与 y的距离定义为| x－ y|。对于 E的任意三个向量 x、 y、 z,有通常关于距离的三角形不等式成立：| x－ z|≤| x－ y|+| y－ z|。
标准正交基
如果欧氏空间的两个向量x与y的内积为零，即(x,y)=0，那么x与y称为正交的。在一个欧氏空间里，与解析几何的直角坐标系相类似的概念是所谓标准正交基。n维欧氏空间E的基e1,e2,…,en,如果满足条件：
那么 e1, e2,…, en称为 E的一个 标准正交基，即 E的一组长度为1且两两正交的基称为标准正交基。任何一个 n维欧氏空间都有标准正交基。如果 e1, e2,…, en是 n维欧氏空间 E的一个标准正交基：
是 E的任意向量，那么：
即在一个标准正交基下，两个向量的内积等于其对应坐标的乘积之和。
欧氏空间的同构
如果两个欧氏空间E和E'，作为实数域上的向量空间是同构的，而且当x↔x',y↔y'时有(x,y)=(x',y'),即E和E'的相对应的向量的内积是相等的,那么E与E'称为同构。任意一个n维欧氏空间都与Rn同构。
酉空间
欧氏空间在复数域上的自然推广。如果V是复数域上的一个向量空间,对于V的任意一对向量u、v，有一个确定的复数(u,v)与之对应,且满足以下条件：(u,v)=(v,u);(u1+u2,v)=(u1,v)+(u2,v); (au,v)=a(u,v);(u,u)≥0,当且仅当u=0时等号成立,那么V称为酉空间。这里u1,u2是V的向量，a是任意复数,(v,u)表示(v,u)的共轭复数。由于有(u,u)=(u,u)，所以(u,u)是实数，因而(u,u)≥0有意义。
在一个酉空间里，也可以把向量u的长|u|定义为
，但是不能像在欧氏空间里那样来定义两个向量的夹角，因为一般说来,( u, v)不一定是实数。尽管酉空间里有向量的长度概念而无夹角概念，然而仍可引入两个向量正交的概念。如果酉空间的两个向量 u、 v的内积为零，即( u, v)=0，那么 u与 v称为正交的。在一个 n维酉空间里,也可以定义标准正交基；而且任一 n维酉空间必定存在标准正交基。
