纤维丛
纤维丛(英语:fiber bundle),可以看作是拓扑乘积的推广。纤维丛概念产生于微分几何的研究。纤维丛的系统研究始于20世纪30年代E.L.斯蒂菲尔、H.惠特尼等对流形上的切丛的研究,它不仅在拓扑学和微分几何学中占有重要地位,也被广泛应用于其他数学和物理学分支。
纤维丛概念
假设空间E是空间X和Y的拓扑乘积。设p:E=X×Y→X为向第一个乘积因子的投影映射,则对于任意x∈X,p−1(x)均同胚于Y。因此E可看作被分解为一族“纤维”{p−1(x)}的联合体。这些“纤维”相互联合的方式是按照已知的乘积拓扑实现的。纤维丛概念是将这种考虑作如下推广。设E,B,F是拓扑空间,p:E→B是连续映射。若对于任意x∈B,p−1(x)均同胚于F,则说E被纤维化为一个以F为纤维型的丛。一般说来,E不是B与F的拓扑乘积。但假设“局部地”是拓扑乘积,即设B中每一点x均有包含x的一个开集Vi,和一个把p−1(Vi)同胚地映成Vi×F的映射φi,使得对每个x∈Vi,φi把p−1(x)映为x×F,E是这些{p−1(Vi)}的并集,因此E可看作是由这些拓扑乘积{Vi×F}拼粘起来的。当Vi∩Vj≠Q时,Vi×F和Vj×F的拼粘方式如下:对每对(x,yi)∈Vi×F,(x,yj)∈Vj×F,x∈Vi∩Vj,如果
- φi−1( x, yi)= φj−1( x, yj)
即( x, yi)= φi φ−1 j( x, yj),就将( x, yi)和( x, yj)粘起来, φi· φj−1是把 x× F映为 x× F的拓扑变换,所以它决定 F的一个拓扑变换 gij( x)。这里 gij( x)· yj= yi,因此 Vi× F和 Vj×F的拼粘就可以看作是借助于一个连续映射
- gij: Vi∩ Vj→ G
来作的,其中 G是 F的一个拓扑变换群,这些 gij称为转移函数。因而就说有了一个纤维丛( E, p, B, F, G),这里E称为全空间, B为底空间, F为纤维型, p为投影, G为构造群。
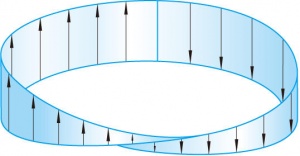
默比乌斯带是最简单的非拓扑乘积的纤维丛。它由一条矩形长带将其一对边中之一扭转180°后与另一边粘合而得。也可看作将一直线段中点放在一个圆周上沿此圆周移动一周的同时,使该线段翻转180°而成。这是一个纤维丛,其全空间E为默比乌斯带,底空间B为圆周,纤维型F为线段,构造群G为F的一个至少包含关于中点的反射在内的拓扑变换群,p:E→B则是将每根直母线映为与B之交点的映射。
切丛
另一类重要的纤维丛。设M是一个实n维微分流形,Tx(M)为M在点x处的切空间,将所有{Tx(M)}用自然方式并起来,得一个2n维微分流形T(M),设P:T(M)→M为将Tx(M)映成x,则得纤维丛(T(M),p,M,Rn,GL(n,R)),称为M的切丛。类似地,还可定义M上的各型张量丛。
截面
连续映射s:B→E称为一个截面,如果s把每个点x∈B映入p−1(x)中。微分流形的切丛的截面是流形上的一个向量场,张量丛上的截面是一个张量场。截面的存在与否是一个重要问题。乘积丛恒有截面,然而由于一般的丛有扭曲,截面不一定存在。例如二维球面的单位切向量所构成的丛没有截面,即球面上切向量场必有奇点。
示性类
纤维丛的截面的存在性问题与阻碍理论有关。由此而得到底空间的某些上同调类,称为示性类,示性类可利用从底空间到分类空间的分类映射将万有丛的示性类(所谓万有示性类)拉回而得到。
示性类中重要者有斯蒂菲尔–惠特尼示性类、陈示性类和庞特里亚金示性类。
吴文俊在示性类理论中有许多重要研究,他发现斯蒂菲尔–惠特尼示性类的斯廷罗德平方运算的表示公式以及微分流形的斯蒂菲尔–惠特尼示性类用吴类表示的公式。
应用
纤维丛理论在微分几何学、代数几何学、复变函数与复流形理论以及大范围分析学等方面有深刻的应用。一般说来,纤维丛是应用代数拓扑学的理论和方法于其他数学领域的一个桥梁。近年来还发现,在物理学中纤维丛是表达规范场的合适的数学语言。