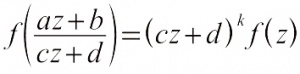费马大定理

费马大定理（英语：Fermat’s last theorem），设n为大于2的整数，则方程 xⁿ+yⁿ＝zⁿ 没有x,y,z全不为0的整数解。又称费马最后定理。大约在1630年，法国数学家P.de费马在丢番图的《算术》的书边的空白处写下了这个著名的定理，并说他找到了一个真正妙不可言的证明，由于空白的地方太小而未写下。在费马的论文中有n＝4时定理的证明。1770年L.欧拉证明了n＝3的情形，n＝5的情形由P.G.L.狄利克雷和A.-M.勒让德证明（1825），n＝7由G.拉梅证明（1839）。可见这个定理证明的进展十分缓慢。容易看出，费马大定理的证明可以归结为n＝4和n为奇素数的情形。n＝4的情形已经解决，因此以下可以假定n＝p（ p为奇素数）。还可以假定x,y,z的最大公因数为1。

1847年，E.E.库默尔对于费马大定理作出了突破性的工作。他基于分圆域的算术理论创造了一种全新的方法，证明了：当p不整除p次分圆域的理想类数时（这种素数称为正则素数），方程x^p+y ^p＝z^p, (xyz, p)＝1没有整数解。这种解称为费马大定理的第一种情形，否则称为第二种情形（无妨假定p|z）。第二种情形比第一种情形要困难得多。之后，人们应用伯努利数、p次分圆域的基本单位、p次分圆域的最大实子域（即与实数域的交）的理想类数等，并用计算机进行大量的计算，对于更多的素数p证明了费马大定理的正确性。到1978年，证明了p＜12 500时，方程x^p+y^p＝z^p没有全不为零的整数解。

1983年德国年轻的数学家G.法尔廷斯用算术代数几何的方法证明了莫德尔猜想。此外还证明了：对于任意的素数p，方程x^p+y ^p＝z^p的整数解的个数有限作为推论。

1985年，D.R.希思–布朗在法尔廷斯的工作的基础上，用解析数论的方法证明了费马大定理对于几乎所有的素数p都成立。

问题的彻底解决开始于1986年。德国数学家G.福瑞发现椭圆曲线的算术理论与费马大定理有关。所谓（有理数域Q上的）椭圆曲线是指三次方程y²＝x³+ax+b (a,b∈Q)所定义的光滑曲线。每一条椭圆曲线都有其L函数。一条椭圆曲线称为模曲线，如果它的L函数在适当的变换下是一个模形式所谓“权为k、水平为N的模形式”是定义在复上半平面上的全纯函数f(z)，满足以下条件：对于任意整数a,b,c,d，如果ad－bc＝1,c≡0(mod N)，则：

其中 k、N 为正整数。假若费马大定理对于某个不小于5的奇素数 p不成立，则存在非零的整数 a, b, c，满足 a  ^p+ b  ^p＝ c  ^p，且( a, b, c)＝1。适当交换 a, b, c的位置及改变它们的正负号，无妨设 a  ^p≡－1( mod 4)， b  ^p≡0(mod 32)。于是就有椭圆曲线 y ²＝ x( x－ a  ^p)( x+ b  ^p)。此曲线称为福瑞曲线。这是一条所谓“半稳定”的椭圆曲线。

如果福瑞曲线是模曲线，则它有太多的性质，借助于B.梅泽尔、R.朗兰兹、J.-P.塞尔、K.A.瑞比特等人的深刻的结果，这些性质能导致存在所谓权2的、水平2的模形式，而事实上这种模形式并不存在。所以只要证明福瑞曲线是模曲线，费马大定理就成立了。

1993年，A.维尔斯在英国剑桥的牛顿数学研究所宣布他证明了半稳定的椭圆曲线是模曲线，从而证明了费马大定理。他证明的核心是发现了二维伽罗瓦表示与模形式之间奥妙的联系。不久，N.卡茨发现维尔斯的证明中有一个漏洞。1995年，R.泰勒和维尔斯合作填补了这个漏洞（实际上，他们证明了更一般的结果）。至此，历史长达300多年的费马大定理终于得以彻底解决。

谷山丰和志村五郎早已猜想所有的定义在有理数域上的椭圆曲线都是模曲线。在维尔斯证明半稳定的椭圆曲线是模曲线之后，2000年，谷山丰–志村五郎猜想被完全证明。

参见

• 数学
• 数学基本条目

• 代数几何学